Article:  Advective mixing in groundwater

Did you learn that streamlines in groundwater flows never intersect? This is absolutely true for two-dimensional divergence-free flows (no source, no sink). In two-dimensional, divergence-free flows the streamline geometry is deformed only locally: at a large distance upstream and downstream from subsurface heterogeneity the streamline arrangement remains exactly the same.

How do streamlines behave in three-dimensional divergence-free flows? In three-dimensional, non-axisymetric flows the streamlines are permanently rearranged by the redistribution of the fluid within the subsurface.

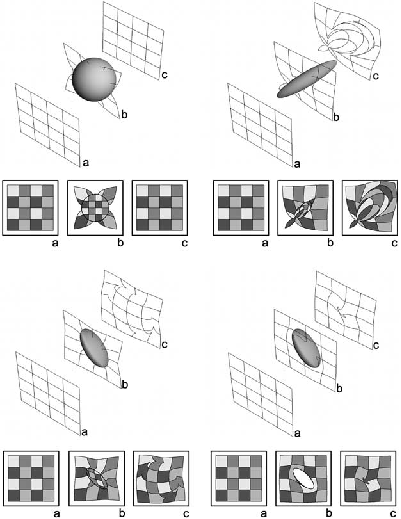
The intersections of stream tubes and control planes for 3-D flow past isolated inclusions: (top left) infinitely conductive sphere, (top right) prolate ellipsoid, (bottom left) oblate ellipsoid, and (bottom right) impermeable oblate ellipsoid (from Jankovic et al., 2009).

What kind of permanent rearrangement can happen?

• streamline focusing/defocusing
• depth-dependent streamline meandering (i.e. streamline deviation),
• secondary motion consisting in persistent twisting, folding, and intertwining of streamlines.

This is called advective mixing and it plays a non-negligible role in enhancing diffusion/dispersion. Modeling subsurface flow transport without accounting for three-dimensional flow and/or small scale heterogeneity will clearly underestimate the subsurface mixing processes.

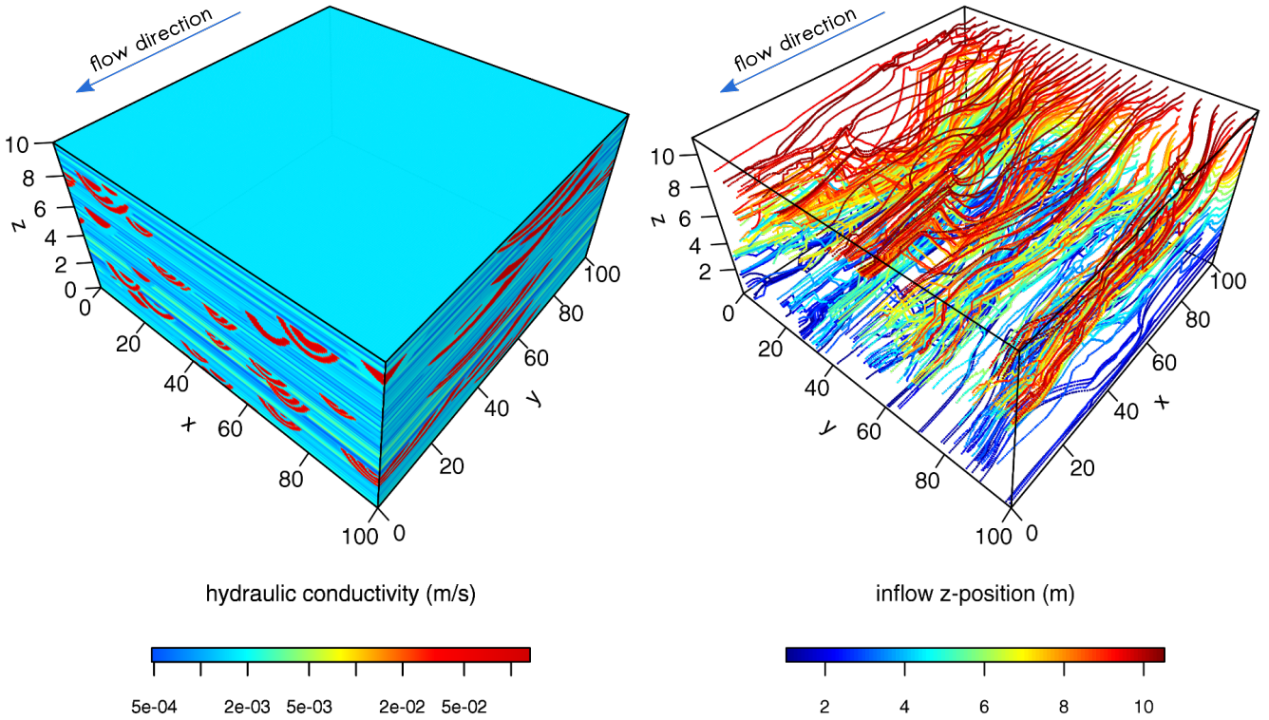
For example, delineating a well capture zone based on a 2D groundwater flow model with particle tracking will result in a too narrow and unrealistic capture zone: in this capture zone a drop of water has a 100% chance to be extracted by the well and the capture zone extends up to the model boundary. In reality the capture chance is decreasing with increasing distance between the drop of water and the well: due to the 3D subsurface flow mixing a drop of water far away from the well has a low chance to reach the well.

Literature about advective mixing:

• Hemker, K., van den Berg, E., and Bakker, M.: Ground Water Whirls, Ground Water, 42, 234?242, DOI: 10.1111/j.1745-6584.2004.tb02670.x, 2004.

• Huber, E. and Huggenberger, P.: Subsurface flow mixing in coarse, braided river deposits, Hydrol. Earth Syst. Sci., 20, 2035?2046, DOI: 10.5194/hess-20-2035-2016, 2016.

• Jankovic, I., Steward, D. R., Barnes, R. J., and Dagan, G.: Is transverse macrodispersivity in three-dimensional groundwater transport equal to zero? A counterexample, Water Resour. Res., 45, W08415, DOI: 10.1029/2009WR007741, 2009.

• Steward, D. R.: Stream surfaces in two-dimensional and three-dimensional divergence-free flows, Water Resour. Res., 34, 1345?1350, DOI: 10.1029/98WR00215, 1998.